Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost) - Škoda

Především matematická mechanika - doprovodné veličiny a vzorce které se uplatňují v mechanice pohybu - což je kinematika a dynamika  - dále rozcestník pro vozy Škoda

obsah příspěvku

1 POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty -  Ludolfovo číslo a  rozměr úhlu jeden RADIÁN

2 mechanika KFD - kinematika-  frekvence a dynamika - úhlová rychlost a rychlost

ÚHLOVÁ RYCHLOST, OTÁČKY ZA MINUTU  a další  druhy veličiny FREKVENCE ve výpočtech funkce motoru a převody mezi nimi

3 mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

ÚHLOVÁ RYCHLOST a TŘI FORMY ČINNOSTI motoru - ROZJEZD s momentem setrvačnosti  - vlastní PROVOZ  s momentem otáčení a VÝKON  motoru sÍ ÚHLOVOU RYCHLOSTÍ  jako přepočtovou veličinou mezi těmito třemi formami

4 MATEMATIKA - INTEGRÁLY A DERIVACE - tři formy činnosti  motoru - ROZJEZD jako derivace nebo podíl - vlastní PROVOZ  jako běžná matematická funkce - rychlost, integrál jako zrychlení a VÝKON  motoru jako kvadratická funkce

rozdíl mezi x a y v rovnici a mezi osou X a y v kartézských souřadnicích   

5? Mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

ČAS A ROZMĚR VE VÝPOĆTECH a TŘI FORMY ČINNOSTI motoru   - ROZJEZD - PROVOZ - VÝKON  a  přeměna veličiny času z potenciálu času před jízdou přepočtem přes úhlovou rychlost na okamžitost výkonu - veličina čas se ve výpočtech vyskytuje ve jmenovateli - kokrétněve frekvenci - časem tedy dělí - na ose x jakoby čas měl hodnotu jedna - a následně jakoby se interval zkracoval - v případě výkonu - promítaného obvykle na osu y se veličinou čas dělí dokonce dvakrát - jelikož jde o exponenciál, či integrál

rozcestníky

matematika obecně
vnitřní matematika – matematika přepočtů (například úhly)
vnější matematika – matematické funkce (i pro jiné obory)
vnější matematika – matematické funkce (i pro jiné obory) integrální a diferenciální počet, exponenciální a logaritmické funkce 
matematika rychlosti a zrychlení (DAV)
podrozcestník rychlost a zrychlení v letectví 
matematika a kybernetika 
automobilismus, motorismus, cyklistika auto - moto - kolo podle značek se zaměřením na vozy ŠKODA
zemědělské stroje, traktory
mechanika pohybu  
kinematika jako mechanika KFD - linie frekvence - rychlost (linie kinematika - dynamika)
kinematika podle druhů (aritmetická, aritmeticko - geometrická, deskriptivně - geometrická konematika)
dynamika jako mechanika DPM - dynamika - linie rychlost, moment síly, výkon
mechanika DPMW - porovnání alternativních výpočtů veličin rychlost, výkon, energie, práce
Mechanika DHM - mechanika hybnosti a méně obvyklých veličin (dvojitých momentů) 
mechanika JB - mechanika jeřábů a bagrů - více praktická verze mechaniky hybnosti
statika

obsah vlastního příspěvku

1 POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty -  Ludolfovo číslo a  rozměr úhlu jeden RADIÁN

2 mechanika KFD RYCHLOSTI - kinematika-  frekvence a dynamika - úhlová rychlost a rychlost

ÚHLOVÁ RYCHLOST, OTÁČKY ZA MINUTU  a další  druhy veličiny FREKVENCE ve výpočtech funkce motoru a převody mezi nimi

3 mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

ÚHLOVÁ RYCHLOST a TŘI FORMY ČINNOSTI motoru - ROZJEZD s momentem setrvačnosti  - vlastní PROVOZ  s momentem otáčení a VÝKON  motoru sÍ ÚHLOVOU RYCHLOSTÍ  jako přepočtovou veličinou mezi těmito třemi formami

rozcestník rozjezd vozidla

4 MATEMATIKA -INTEGRÁLY, běžné matematické FUNKCE  a DERIVACE a TŘI FORMY ČINNOSTI motoru - tři formy činnosti  motoru - ROZJEZD jako derivace nebo podíl - vlastní PROVOZ  jako běžná matematická funkce pro rychlost a INTEGRÁL pro zrychlení - a VÝKON  motoru jako kvadratická funkce

rozdíl mezi x a y v rovnici a mezi osou X a y v kartézských souřadnicích   

5 Mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

ČAS A ROZMĚR VE VÝPOĆTECH a TŘI FORMY ČINNOSTI motoru   - ROZJEZD - PROVOZ - VÝKON  a  přeměna veličiny času z potenciálu času před jízdou přepočtem přes úhlovou rychlost na okamžitost výkonu - veličina čas se ve výpočtech vyskytuje ve jmenovateli - kokrétněve frekvenci - časem tedy dělí - na ose x jakoby čas měl hodnotu jedna - a následně jakoby se interval zkracoval - v případě výkonu - promítaného obvykle na osu y se veličinou čas dělí dokonce dvakrát - jelikož jde o exponenciál, či integrál

 

 

anotace na úvod

poměrně důležitá v kinematice i dynamice - je veličina frekvence (což je celá otáčka za vteřinu i odvozené veličiny - úhlová frekvence k radiánu a úhlová rychlost - neboli frekvence k proměnlivému úhlu nebo RPM otáčky za minutu) jako veličina není vlastně nic jiného - než rotující hmotný bod, jako například sonda v ose bicyklu 

tento příspěvek se věnuje spíše  doplňkovým výpočtům v mechanice pohybu - například přepočtům úhlů - neboť některé druhy frekvence se vztahují například k radiánům (úhlová frekvence omega) - jiné zase k celému úhlu  (například - jak již bylo výše naznačeno "standartní" frekvence k 360 stupňům, která lze rovněž vyjádřit jako otáčky za minutu - RPM)

doplňkové matematické výpočty pro mechaniku zde jsou označovány jako  "matematická mechanika"

hlavním příspěvkem pro standartní kinematiku - dynamiku (tedy přepočty veličin frekvence - rychlost - tlak - síla - moment setrvačnosti - moment otáčení - výkon) tedy hlavním příspěvkem pro mechaniku pohybu a současně značku ŠKODA jsou příspěvky... 

kinematika a dynamika 1

Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola/ osobní automobily Škoda - Blog iDNES.cz Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to? - čímž by se měl zabývat odkazovaný příspěvek, tedy zejména veličinami úhlová dráha a úhlová rychlost OMEGA.

dynamika 1

Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz

dynamika 2

Mechanika DPM 2/W čím se liší veličiny tlak - síla a práce? - nákl. vozy Škoda / Praga / Liaz - Blog iDNES.cz

rozdělení příspěvků na téma matematika

mechanika pohybu - kinematika a dynamika

A1 (kinematika1 i dynamika 1) Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz

A1D (dynamika 1) Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz

A2 rozjezd nákladních automobilů 2 (dynamika 2) Mechanika DPM 2/W čím se liší veličiny tlak - síla a práce? - nákl. vozy Škoda/Praga - Blog iDNES.cz

A3(kinematika3 i dynamika 3)  rozjezd vozidla  různé druhy frekvence podrobněji a současně příspěvek nákladní automobily 3 (rychlá nákladní vozidla typu sanitka), či rozjezd vozidel 1 Mechanika A1/KFD - rychlá nákladní vozidla - sanitky  a jejich rozjezd (1) přepočty druhů frekvence - Blog iDNES.cz

matematika obecně

tento příspěvek je vlastně úvodním příspěvkem a na téma matematika s označením "A"

A vstupní (tento) příspěvek pro matematiku - se zaměřením na doplňkové výpočty (např. přepočet úlových měr, druhů frekvence) v mechanice pohybu

A0 hlavní příspěvek pro matematiku a mechaniku pohybu a současně VUT Brno  Mechanika A0/ KFD 0 rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu - Blog iDNES.cz" rovněž přepočty: obvod kola (rychlost) - obvod kola (síla); osa kola (úhlová rychlost) - osa kola (moment otáčení); osa kola (úhlová rychlost) - obvod kola (rotační rychlost a rychlost celého vozidla); osa kola (moment otáčení) - obvod kola (síla nebo rotační rychlost) 

A3 různé druhy frekvence podrobněji a současně příspěvek sanitky  (rychlá nákladní vozidla), či rozjezd vozidel 1 Mechanika A3/KFD - rychlá  vozidla a jejich rozjezd (3) přepočty druhů frekvence - Blog iDNES.cz

Avia“	Mechanika A3/KFD - radián, druhy frekvence, nákladní vozidla Avia a jejich rozjezd 3 - Blog iDNES.cz	radiánfrekvence
	C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz	úhlů,––,,
A2	Mosty od klenbových po vysuté (statika 2) - soustava staticky (ne, pře) určitá - Blog iDNES.cz
	Návštěva staré tiskárny - části strojů a mechanismy - rozcestník pro průmysl - Blog iDNES.cz
„“	A11V Eulerova konstanta, sinus, cosinus, Pythagorova věta  (Co se děje kolem matematiky,11) - Blog iDNES.cz

vnitřní matematika – matematika přepočtů

	Mechanika A0/ KFD 0 rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu - Blog iDNES.cz
A
A11V	A11V Eulerova konstanta, integrály a derivace (Co se děje kolem matematiky 11) - Blog iDNES.cz
A3Avia“radián	Mechanika A1/KFD - radián, druhy frekvence, rozjezd a výkon sanitky - Blog iDNES.cz
C1přepočtyúhlů,––,,	C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz

...a klíčový příspěvek - matematika a mechanika rychlosti a zrychlení Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to? - čímž by se měl zabývat výše zmíněný příspěvek , tedy zejména veličinami úhlová dráha a úhlová rychlost OMEGA.

vnější matematika – matematické funkce (i pro jiné obory)

A11V	A11V Rovnice, funkce, derivace, integrály, logaritmy - Blog iDNES.cz
AV	Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů AV - Blog iDNES.cz
AVE	Cesty elektrické energie a Ohmův zákon 2 - elektrárna Oslavany, Západomoravské elektrárny - Blog iDNES.cz
	Co se děje kolem elektřiny 7 - Ohmův zákon (2) a tři verze pro zapojený obvod, osciloskop - Blog iDNES.czelektrotechnikamatematickáderivace)
	Matematické úvahy u sázení brambor - Blog iDNES.cz

 

vnější matematika – matematické funkce (i pro jiné obory)

integrální a diferenciální počet 

AVs integrální a diferenciální počet  slovesně "AVs" Matematická zamyšlení aneb jak se sází brambory a vaří bramborový guláš - Blog iDNES.cz / A4s pravé a nepravé dělení (porcování a poměřování) Mechanika DAV(PM): Holešov - rychlost letounu Z 142 - okamžitá a statistická ,zrychlení - Blog iDNES.cz

AVNádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů "AV - Blog iDNES.cz

A11VA11V Rovnice, funkce, derivace, integrály, logaritmy, a Eulerova konstanta - Blog iDNES.cz

AVECesty elektrické energie a Ohmův zákon 2 - elektrárna Oslavany, Západomoravské elektrárny - Blog iDNES.cz

matematika rychlosti a zrychlení

Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz zrychlení automobilu

hlavní příspěvek matematické funkce, rovnice a rychlost zrychlení AV Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů AV - Blog iDNES.cz

podrozcestník rychlost a zrychlení v letectví 

kinematické přepočty otáčky - rychlost - na pístovém motoru i tachometru (tedy spíše obor kinematika) Letoun Avia Av-57, jak se počítá na tachometru rychlost letounu 4 - Blog iDNES.cz-  čtvrtá verze příspěvku 

matematické přepočty rychlost z letu a statistická rychlost Mechanika A/ DAV (PM) - matematika slovesně, rychlost, zrychlení, vzlet 1, katalog letišť - Blog iDNES.cz třetí verze příspěvku 

veličiny rychlost, zrychlení a výkon (tedy spíše obor dynamika) Jak měří letecký tachometr rychlost letounu 2, letiště Žatec a Mig 29, mechanika DPMW - Blog iDNES.cz druhá verze příspěvku 

veličiny frekvence, rychlost, zrychlení především z hlediska matematiky Mechanika DAV(PM): Holešov - rychlost a zrychlení letounu Z 142, skoky padákem - Blog iDNES.cz) - první verze příspěvku

podrozcestník rychlost a zrychlení jako veličiny dynamiky

Mechanika DAV (PM)  - dynamika - rychlost a zrychlení

spíše studijní příspěvek jak vysvětlit vytváření rychlosti a zrychlení jako veličin, některé názory jsou již v příspěvku překonány Mechanika A/ DAV (PM) - matematika slovesně 1, zrychlení neboli vzlet, katalog letišť - Blog iDNES.cz

příspěvek zaměřený především na zkoumání rychlosti, pokračování předchozího, tedy výpočet rychlosti   Letecké měřící přístroje a odpovídající veličiny 2, letiště Žatec a Mig 29 - Blog iDNES.cz

zejména rozdíl rychlost - úhlová rychlost - frekvence v příspěvku Mechanika a elektrotechnika 17 - jak se děje jeví uvnitř a vně - zejména pak frekvence - Blog iDNES.cz

matematika a kybernetika 

Ac odkaz na rozcestník matematika a kybernetika  V zajetí počítačů, elektroniky a kybernetiky 4 - Blog iDNES.cz

Ac3 V zajetí počítačů 3 (matematická logika a technika, logická hradla logické funkce) - Blog iDNES.cz

konjukce (logický součin průnik) - hradlo "and"
disjunkce (logický součet) - hradlo "or"
Shefferova spojka (negace logického součinu)  - hradlo "nahd

rozdělení příspěvků na téma mechanika

Automobilismus, motorismus, cyklistika

auto - moto - kolo podle značek se zaměřením na 

vozy 

ŠKODA

osobní vozy

Laurin a Klement, Škoda

(osobní vozy 1) 

kinematika a dynamika jezdec "0", pastorek "první kolo v převodu 1", "druhé kolo převodu "2", kolo vozidla a silnice "3" Mechanika KFD1 / DAV - frekvence, rychlost, zrychlení / kinematika fotbalového míče / proč rychlé vozy mají velká kola - Blog iDNES.cz s současně druhý příspěvek pro původně pro automobilovou opravnu vozů Škoda (Representace Škodových závodů v Jihlavě v Žižkově ulici)

(nákladní vozy 2) nákladní vozidla různých  českých  značek (Škoda, Praga, Avia  Liaz  - i užitkvá) Mechanika DPM 2 /W výkon z tlaku, ze síly nebo práce? - nákladní vozy 2 - Blog iDNES.cz s současně třetí příspěvek pro původně pro automobilovou opravnu vozů Škoda (Representace Škodových závodů v Jihlavě v Žižkově ulici)

(nákladní vozy 3) rychlé nákladní vozy a sanitky Avia při rozjezdu   Mechanika A3/ KDF3  rychlá nákladní vozidla a jejich rozjezd 1moment setrvačnosti,  - přepočet různých druhů frekvence při rozjedu - úhlová k radiánu, celoúhlová frekvence k 360 a RPM - otáčky za minutu "  - Blog iDNES.cz který zároveň pojednává o obloukových mírách ( A" oddíl 2-  RADIÁN PŘI PŘEPOČTECH RŮZNÝCH DRUHŮ FREKVENCÍ A VÝKON A TOČIVÝ MOMENT) a tvoří dvoupříspěvek s příspěvkem Mechanika A/ KFD - Ludolfovo číslo a radián - přepočty různých druhů frekvence - Blog iDNES.cz

Mercedes - Benz, vojenská vozba

Převody mechanické (pastorek a kolo) a elektrické (trafa) - vozy Mercedes a vojenství - Blog iDNES.cz

BMW https://www.facebook.com/media/set/?set=a.5320012821396763&type=3

cyklistické, motocyklové, automobilové sporty

"Cyklistika 1 (motokola)" podle továrních značek Mechanika A/DPMW: stupně, Ludolfovo číslo a radiány a přepočet rychlosti bicyklu - Blog iDNES.cz

"Cyklistika 2" cyklistické pohony a motory - cyklistické a motoristické závody Mechanika KFD 2 - pomaluběžný nebo rychloběžný motor, cyklistické závody - Blog iDNES.cz

silniční motocykly Původní Masarykův okruh a Velká cena 1984 - Blog iDNES.cz, Velká cena Brna a motocykly Kawasaki - Blog iDNES.cz

různé druhy motocyklových pohonů, silniční cyklistika, sálová cyklistika, motokros, enduro Mechanika KFD 2 - pomaluběžný nebo rychloběžný motor, cyklistické závody - Blog iDNES.cz

cyklokros, šlapačky Oblouková míra - stupně, Ludolfovo číslo a radiány a přepočet rychlosti vstup - výstup - Blog iDNES.cz součástí příspěvku je také alternativní výpočet rychlosti z frekvence nebo dráhy, a také výpočet vstupní a výstupní rychlosti bicyklu

zemědělské stroje, traktory

Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz

Letní čtení na táboře a krásné staré zemědělné stroje - rozcestník Vysočina - Blog iDNES.cz stručná historie traktorů Zetor

stavební stroje 

Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz rozdělení stavebních strojů podle  knihy "Motorové opojení"

Mechanika pohybu

kinematika

Mechanika KFD - linie frekvence - rychlost (linie kinematika - dynamika)

mechanika KFD 1 kinematika základních přepočtů 

úvodní příspěvek - osobní, případně automobilové závodní vozy - rychlé vozy "velká kola" Mechanika KFD1 - perioda, frekvence, obvodová rychlost / proč rychlé vozy mají velká kola - Blog iDNES.cz  příspěvek by také mohl mít název čím se liší tachometr a otáčkoměr (zde se zkoumá rychlost a zrychlení) a protože značná část příspěvku je věnována přepočtům perioda  frekvence  rychlost mohl by se příspěvek rovněž nazývat mechanika KFD

mechanika KFD 2 kinematika pohonů Mechanika KFD 2cm - pomaluběžný nebo rychloběžný motor, cyklistické závody - Blog iDNES.cz "traktory a nákladní vozy " Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz dvoupříspěvek s tímto příspěvkem  Mechanika DPM 3 /W výkon okamžitý z frekvence a statistický z práce - nákladní vozy 3 - Blog iDNES.cz "sesterský příspěvek " - moment síly - tedy záběr síly má maximum na středu kola, proto také tahače mají povícero kol o nevelkém průměru - přepočet úhlové rychlosti a momentu setrvačnosti a otáčení

Mechanika KFD 3 (také cyklistika a motorismus) a kinematika druhů   Mechanika - kinematika  A/ KFD 3 rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu - Blog iDNES.cz příspěvek srovnává především dva zdroje pohybu - statickou sílu - ze které plyne moment síly (z něhož částečně vyplývá i soustružnický efekt) a kinematickou sílu - ze které zase vyplývá rychlost 
aritmetická kinematika - otáčky pohonu (například motoru automobilu)

aritmeticko - geometrická  kinematika - čas přepočtený na úhlovou dráhu - může mít význam například u výpočtu otáček kladkostroje; (aritmeticko) - geometrická kinematika například pro pohyb kladkostrojea  určité míry  i stavebních strojů j jeřábů  - kinematika která vychází z frekvence a hybnosti 

deskriptivně - geometrická  kinematika - čas zde nehraje roli - význam zde mají úhly mezi jednotlivými elementy a také počet stupňů volnosti příslušný ke každému elementu - typickým zařízením kde se uplatňuje tato disciplína jsou stavební stroje a jeřáby

Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz

Mechanika KFD 4podle dráhy a trajektorie / podle dráhy /podle obálky / podle polodií  Návštěva staré tiskárny - části strojů a mechanismy - Blog iDNES.cz

Mechanika KFD 6 "horské dráhy a lanovky" Horské a lanové dráhy v Čechách a blízkém zahraničí - mechanika KFD - Blog iDNES.cz

společné přepočty pro veličiny mechaniky pohybu KFD/DPM

přepočty veličin hřídel / obvod - např. úhlová rychlost na ose - obvodová rychlost nebo moment síly - síla Mechanika A3/ KFD 3 rozcestník matematická mechanika a jak měří siloměr přes rychlost sílu - Blog iDNES.cz

inverzní moment síly, který se zvětšuje k obvodu (?) neblaze proslulá hranatá okénka u letounu Comet de Havilland kde se na okrajích vytvářely mikroskopické praskliny Paní Simpsonová a Goethe / De Havilland DH 106 Comet - Blog iDNES.cz

dynamika

Mechanika DPM - dynamika - linie rychlost, moment síly, výkon

přepočet sil, momentů, rychlostí na ose i na obvodu a výkonu (mechanika DPM) na kole vozu i celém vozidle

"první díl"  Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz (přepočet síla a momenty) - v části 3 odkazovaneho příspěvku

"druhý díl" pokračování přepočtů "druhý díl" - se zaměřením úhlová rychlost, moment setrvačnosti a moment otáčení na ose - a síla na obvodu kola v příspěvku Mechanika DPM 3 /W moment setrvačnosti /úhlová rychlost - moment síly - síla / výkon okamžitý z frekvence a statistický z práce - nákladní vozy 3 - Blog iDNES.cz(v části 3 odkazovaného příspěvku)

a další pokračování "třetí díl" - kde přepočty doplní i přepočet úhlová rychlost - rotační rychlost a síla  na obvodu  Mechanika KFD / DAV - frekvence, rychlost, zrychlení / kinematika fotbalového míče / proč rychlé vozy mají velká kola - Blog iDNES.cz 

+ společný příspěvek pro mechaniku a elektrotechniku 

Mechanika - elektrotechnika MFE 5 - výkon - jako moment třetího stupně, kruhový diagram - Blog iDNES.cz

Mechanika DPMW - porovnání alternativních výpočtů veličin rychlost, výkon, energie, práce

naopak zcela počáteční příspěvek na dané téma, některé názory jsou již v příspěvku překonány Mechanika A/ DAV (PM) - matematika slovesně, zrychlení neboli vzlet, katalog letišť - Blog iDNES.cz

pravděpodobně nejpropracovanější příspěvek, je zde zobrazeno celé spektrum veličin -  moment otáčení, výkon a další veličiny Mechanika DPM/W výkon okamžitý z frekvence, nebo statistický z práce - nákladní vozy - Blog iDNES.cz

Mechanika DHM - mechanika hybnosti a méně obvyklých veličin (dvojitých momentů) 

Mechanika DHM - hybnost, moment hybnosti, změna hybnosti a letouny Iljušin v Brně Slatině - Blog iDNES.cz

Mechanika JB - mechanika jeřábů a bagrů - více praktická verze mechaniky hybnosti

Mechanika JB /DPMW přístavní jeřáb - jak se připojit k internetu 4 (přirovnání k přístavu) - Blog iDNES.cz

Mechanika JB2 - Cesty elektrické energie 8 (pojistky 3 + mostové jeřáby) - Blog iDNES.cz

Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů - Blog iDNES.cz

Statika

Mechanika SK  - statika staveb a konstrukcí

Cesty elektrické energie 10/ stavba 3 - rozvody a stavba - administrativa a výkres - Blog iDNES.cz

Mechanika SM  - statika mostů

Statika 1 - mosty 1 + 1 (oddělený ohyb mostovky a tlak podpory), vojenské stavby - Blog iDNES.cz

znovu přehled témat

matematika obecně
vnitřní matematika – matematika přepočtů (například úhly)
vnější matematika – matematické funkce (i pro jiné obory)
vnější matematika – matematické funkce (i pro jiné obory) integrální a diferenciální počet 
matematika rychlosti a zrychlení (DAV)
podrozcestník rychlost a zrychlení v letectví 
matematika a kybernetika 
automobilismus, motorismus, cyklistika auto - moto - kolo podle značek se zaměřením na vozy ŠKODA
zemědělské stroje, traktory
mechanika pohybu  
kinematika jako mechanika KFD - linie frekvence - rychlost (linie kinematika - dynamika)
kinematika druhů (aritmetická, aritmeticko - geometrická, deskriptivně - geometrická konematika)
dynamika jako mechanika DPM - dynamika - linie rychlost, moment síly, výkon
mechanika DPMW - porovnání alternativních výpočtů veličin rychlost, výkon, energie, práce
Mechanika DHM - mechanika hybnosti a méně obvyklých veličin (dvojitých momentů) 
mechanika JB - mechanika jeřábů a bagrů - více praktická verze mechaniky hybnosti
statika

tedy vlastní příspěvek

Mechanika A/ KFD : kinematika (frekvence),  dynamika (úhlová a obvodová rychlost) - Škoda

 

CO SE VLASTNĚ ZJIŠŤUJE A POČÍTÁ

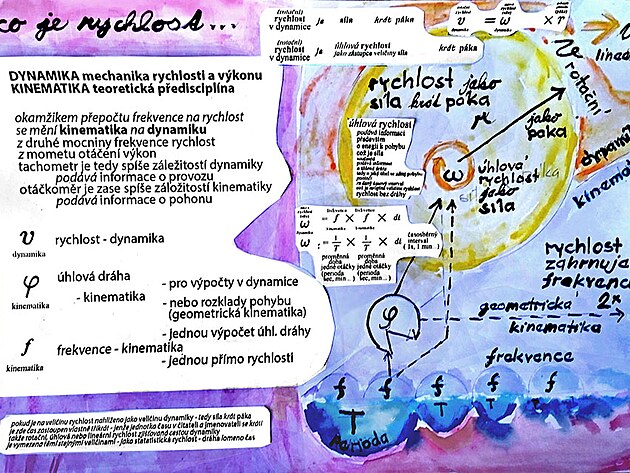
poměrně důležitou veličinou v mechanice pohybu je tzv. úhlová rychlost OMEGA na ose hřídele - vzhledem k faktu - že pohyb se takřka vždy přenáší přes hřídel - je otáčivý potenciál hřídele vlastně vystihuje mechanické pohybu vůbec nejvíc - do rotačního pohybu na ose - úhlové rychlosti OMEGA se vlastně promítají všechny další veličiny mechaniky - síla i moment síly, frekvence i obvodová rychlost i výkon - úhlová rychlost by sedala vyjádřit jak v sekundách - přesněji hercích - tak Newtonech - přesněji odmocnině Newtonů

vzhledem k faktu že v mechanice pohybu se takřka vždy vyskytuje v nějaké formě rotační pohyb, který zahrnuje třeba část kruhu či kružnice - s mechanikou pohybu souvisí řada přepočtů týkajících se úhlových měr - a také přepočtů mezi různými druhy veličin které definují rychlost pohybu - jako frekvence, perioda, úhlová rychlost na ose - i rychlost obvodová a lineární 

VLASTNÍ PŘÍSPEVEK

část 1

 

1 POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty -  Ludolfovo číslo a  rozměr úhlu jeden RADIÁN

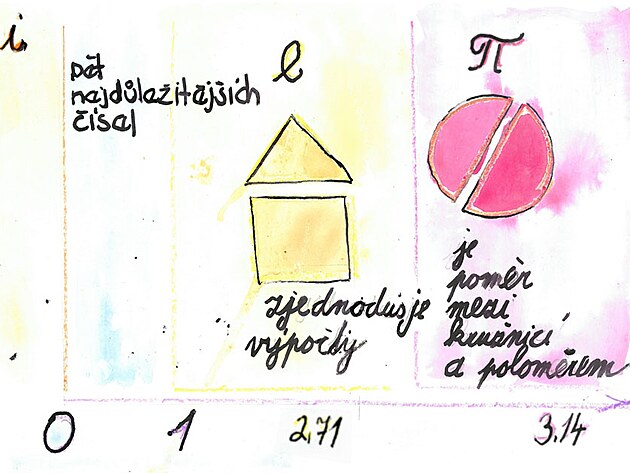
Radián patří mezi pět nejdůležitějších čísle v matematice - kam tedy patří zmíněné Ludolfovo číslo, Eulerovo číslo, jedna, nula a imaginární jednotka. 

rozcestník matematika doplňkových výpočtů 

Ludolfovo číslo a radián 1A Mechanika A/ KFD : kinematika (frekvence),  dynamika (úhlová a obvodová rychlost) - Škoda (tento příspěvek)

Ludolfovo číslo a radián 1C C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz

Ludolfovo číslo a radián 3 Mechanika A3/KFD - radián, frekvence, rozjezd a výkon sanitky, rozcestník Avia - Blog iDNES.cz

Eulerova konstanta A11V Rovnice, funkce, derivace, integrály, logaritmy, a Eulerova konstanta - Blog iDNES.cz

část 1 1 POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty -  Ludolfovo číslo a  rozměr úhlu jeden radián

část 1 1 RADIÁN původní verze - ÚVOD

původní (pracovní) teze převzatá z předchozích příspěvků

RADIÁN je

1. jednotka úhlu 1rad ´= 57.30 st
2. jenotka délky obloku 1 rad ´= 1 metr
(3. radián je pravděpodobně i funkce - nebo figuruje ve vzorci pro výpočet délky oblouku - vzdálená obdoba goniometrických funkcí)

specifikem radiánu tedy je 

všechny rozměry (úhel, úsečka poloměru a oblouk) jsou rovny "jedné" 

PROČ TEDY RŮZNICE V INERPRETACI RADIÁNU?

Možná někdo jiný v úvozovkách "vymyslel" radián jako úhlovou jednotku a někdo jiný zase definici..

část 1 1 RADIÁN původní verze  - POKRAČOVÁNÍ

RADIÁN SE HLAVNĚ UPLATŇUJE VE DVOU ODLIŠNÝCH ÚČELECH

část 1 1 RADIÁN původní verze  - FREKVENCE pro výpočet frekvencí (úhlová frekvence, úhlová rychlost, obvodová frekvence, otáčky za minutu - se výpočty provádějí s RADIÁNEM JAKO ÚHLEM

FREKVENCE A ÚHLY JSOU RELATIVNÍ HODNOTOU

1 RADIÁN původní verze  - OBVOD KRUŽNICE.. pro výpočet délky obvodu kružnice - například OBVODU OZUBENÉHO KOLA se počítá s radiánem jako DÉLKOVOU JEDNOTKOU 

při úhlu 1 RAD je DÉLKA POLOMĚRU stejná jako DÉLKA OBLOUKU pro 1 RAD

2? rad ? 2? r

úhel není obvod

z čehož plyne 2 Pí R ´=  2 Pí L (délka oblouku) - tento vzorec se používá právě pro výpočet obvodu a točícího momentu

OBVOD OZUBENÉHO KOLA, OBVODOVÁ RYCHLOST a potažmo i MOMET TOČENÍ, nepřímo i (obvodová) SÍLA - pro jejichž výpočet je zásadní znalost DÉLKY OBVODU KRUŽNICE ozubeného kola jsou tzv. ABSOLUTNÍMI HODNOTAM

ještě upřesňující teze na základě poznámek Pouze při vhodně zvoleném poloměru kružnice je radián ČÍSLO - číslo úhlu v radiánech je stejné, jako délka oblouku v metrech 

další příspěvky na téma přepočty úhlů

A1Avia“	Mechanika A1/KFD - radián, druhy frekvence, rozjezd a výkon sanitky - Blog iDNES.cz
C1přepočtyúhlů,––,,	C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz

PŘEVOD MEZI OBVODEM A POLOMĚREM KRUŽNICE

část 1

1 RADIÁN - novelizace - PŘEVOD MEZI OBVODEM A POLOMĚREM KRUŽNICE

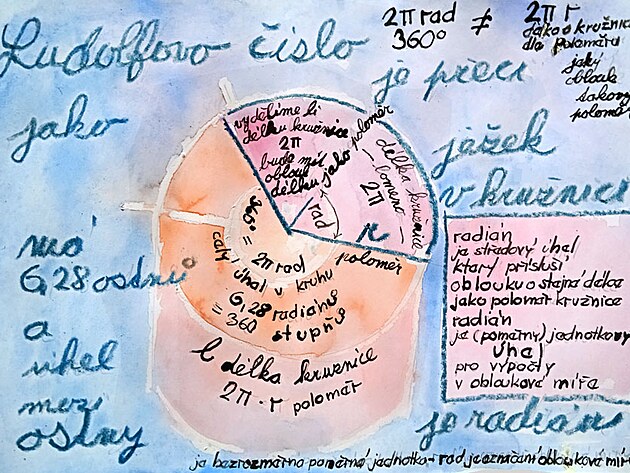
Podle různých pramenů (wikipedie)  je radián jednotkou obloukové míry. Jedná se o bezměrnou poměrnou jednotku. Pro tuto bezrozměrnou jednotku se používá označení radián, Radián jako poměrná jednotka je ovšem definován jak rovínný úhel se stanoveným přrevodem na úhlovou míru ve stupních 1RAD = 57.67 stupňů.

Jak mohl radián vzniknout.

Možná si někdo mohl všimnout, že mezi obvodem kružnice a jejím poloměrem je stálý poměr - i když velikost kružnice se mění. A možná zkusil tento poloměr vyjádřit podělením obvodu poloměrem. 

délka kružnice

----------------------------- lomeno -----------------------------

poloměr kružnice

=== je rovno ===

6. 28 neboli 2 x 3. 14

a pro tento poměr, přesněji číslo poměru se ujalo označení
Ludolfovo číslo

a převodový poměr mezi obvodek kružnice a poloměrem je tedy

2?

a pokud se kružnice rozčlení 

na 2? neboli  6.28 výsečí

v středu těchto výsečí s vytvoří úhel 57,67 stupňů

a pro výpočty různých úhlových veličin jako =uhlová rychlost OMEGA, úhlová frekvence OMEGA , moment otáčení, výkon se pravděpodobně pro zjednodušení 

místo jiných úhlových měr 

začala užívat číslice "1" 

pro niž se ujalo označení RADIÁN

velmi podobný vzorec jako pro výpočty úhlových jednotek (frekvence, výkon .atd)

je i pro výpočet obvodu

2? rad ? 2? r

úhel není obvod

ale pro výpočet obvodu nebo oblouku není u tohoto vzorce označení RADIÁN užívat, protože se vlastně jedná o převodový poměr mezi obvodem kružnice a poloměrem daný právě číslicí 2? která nemá jiný význam než-li cifru 6.28

konec části 1 POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty -  Ludolfovo číslo a  rozměr úhlu jeden radián

další příspěvky na téma přepočty úhlů

A1Avia“	Mechanika A1/KFD3 - radián, druhy frekvence, rozjezd a výkon sanitky - Blog iDNES.cz
C1přepočtyúhlů,––,,	C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů - Blog iDNES.cz

 v automobilismu se nejčastěji udávají otáčky za minutu RPM - což je vlastně obvodová frekvence převedená z otáček za vteřinu na otáčky za minutu

jaké jsou tedy druhy frekvencí?

část 2 FREKVENCE a  RYCHLOST v kinematice  

Z HLEDISKA MECHANIKY POHYBU je jako VÝHODNĚJŠÍ  než veličinu SÍLA brát VELIČINU RYCHLOST - neboť RYCHLOST - ZEJMÉNA ROTAČNÍ (ostatně teoreticky

 i proud trysky leteckého motoru má původ v rotaci - a to rotaci kompresoru) - z hlediska MECHANIKY,  je tedy  jako PŘESNĚJŠÍ BRÁT VELIČINU RYCHLOST - NEBOŤ RYCHLOST JE RYTMIZOVÁNA - MOŽNO ŘÍCI ČLENĚNA NA DÍLČÍ KINEMATICKÉ VELIČINY - JAKÝMI jsou MOMENT OTÁČENÍ "Torque "(který má stejný průběh od osy k obvodu - jak ostatně definuje MOMENTOVÁ VĚTA) - dalšími veličinami v posloupnosti je pak tzv. ÚHLOVÁ RYCHLOST OMEGA na ose hřídele - možná přesnější označení by bylo označení ZÁBĚR OMEGA - neboť záběr na ose zahrnuje jak veličiny RYCHLOST a SÍLA - ale nezahrnuje poloměr kola (ostatně úhlová rychlost OMEGA tak trochu připomíná pádlování třeba na kajaku - nebo kanoi) - tedy pomyslná střed záběru mezi konci pádla) - pokud by se v členění kinematických veličin postupovalo ještě dále - tak dalšími veličinami v posloupnosti níže pod ÚHLOVOU RYCHLOSTÍ OMEGA  na ose hřídele by byly veličiny frekvence/perioda - veličina úhlová dráha "Fí" - která představuje něco jako natažení hodin - a která s největší pravděpodobností by byla jednou z cest přepočtu veličiny SÍLA na RYCHLOST - druhou cestou by měl být přepočet rychlosti a síly přes MOMENT OTÁČENÍ. 

jednotlivé druhy frekvencí - jako frekvence jsou udávány tři (nepřesně čtyři) veličiny

f
RPM

Otázka zní - dva hráči kopnou do dvou míčů - nebo udeří do koule kulečníku - na začátku se míče kotálí se stejnou frekvencí - jeden se však rychleji zpomalí - a druhý dokotálí dál ... proč to? - čímž by se měl zabývat obdobný příspěvek Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz  , tedy zejména veličinami úhlová dráha a úhlová rychlost OMEGA.

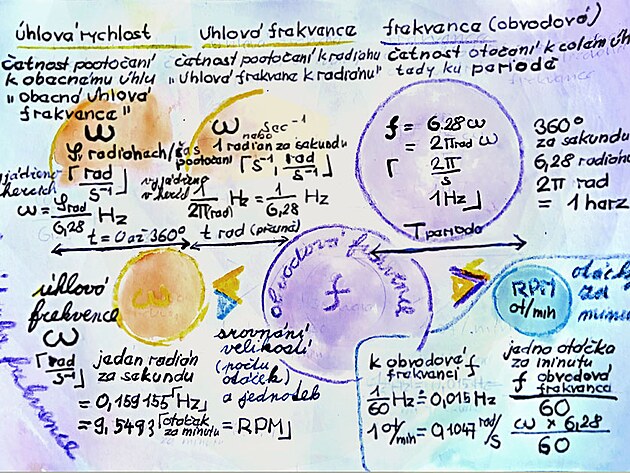
2,1 úhlová rychlost "omega" - počet otáček za sekundu k obecnému úhlu - obecná úhlová frekvence v radiánech za sekundu

úhlová rychlost - obecná úhlová frekvence je výchozí veličina pro výpočet úhlové rychlosti (a pří znalosti konkrétního poloměru) pak i obvodové rychlosti např. ozubeného kola - další přepočtem by se dalo dobrat i (lineární) rychlosti celého vozu

část 2 FREKVENCE

2,2 úhlová frekvence "omega" - počet otáček za sekundu k radiánu - úhlová frekvence k radiánu v radiánech za sekundu nebo vlastně jensekundách na mínus prvou (v převrácených sekundách)

část 2 FREKVENCE

2,3  frekvence "f" , obvodová frekvence v herzích - přesnějifrekvence k úhlu celého obvodu tedy k úhlu 2Pí  rad,  neboli 6.28 rad - neboli 360 stupňů - pro výpočet frekvence f není potřeba znalost obvodu ani poloměru - jedná se vlastně o přepočet úhlové frekvence na celý obvod    - zkratka 2Pí nemá žádný matematický význam jedná s o hodnotu úhlu psanou v radiánech - sejnou platnost by měla veličina udaná v jiné úhlové míře - stupních, gradiánech atd

část 2 FREKVENCE

2,4  otáčky za minutu  "RPM" - frekvence 

frekvence k úhlu celého obvodu převedená ze sekund na vteřiny

konec části 2 ÚHLOVÁ RYCHLOST, OTÁČKY ZA MINUTU  a další  druhy veličiny FREKVENCE ve výpočtech funkce motoru a převody mezi nimi

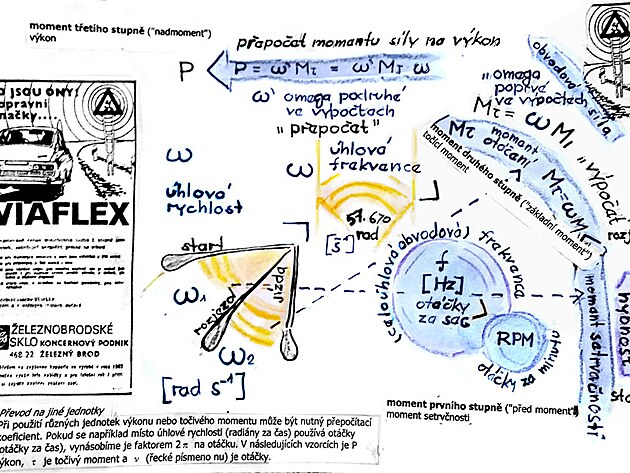
část 3 - UHLOVÁ RYCHLOST (vnitřní rotace OMEGA) - MOMENT SÍLY (moment 1. stupně) a VÝKON (moment 2. stupně)

bádání níže bylo již v řadě závěrů překonáno - obsahuje řadu záměn témat - aktuálnější - a snad i přesnější závěry v odkazech 

rozcestník rozjezd vozidla 1 a osobní automobily Škoda

rozjezd vozidla 2 a nákladní automobily Škoda / Praga Mechanika DPM 3 /W výkon na ose z tlaku a práce - nákladní vozy Škoda - Blog iDNES.cz současně album nákladních vozů Škoda

rozjezd vozidla 3 a sanitky AVIA Mechanika A3/KFD - radián, frekvence, rozjezd a výkon sanitky, rozcestník Avia - Blog iDNES.cz

tato část příspěvku spadá do tématického okruhu Mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

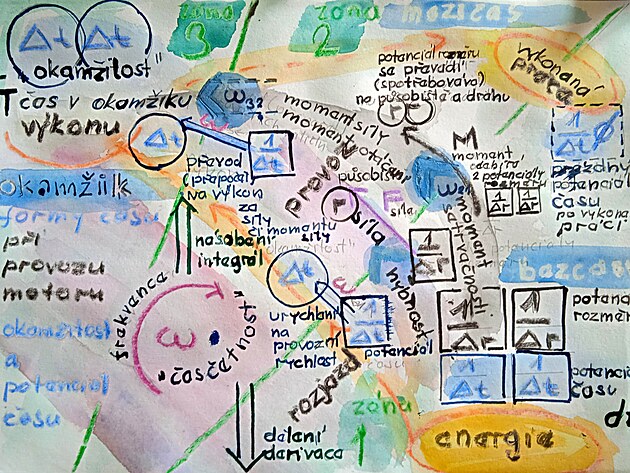
3 ÚHLOVÁ RYCHLOST (vnitřní rotace OMEGA)  TŘI FORMY ČINNOSTI motoru - ROZJEZD s momentem setrvačnosti  - vlastní PROVOZ  s momentem otáčení a VÝKON  motoru sÍ ÚHLOVOU RYCHLOSTÍ  jako přepočtovou veličinou mezi těmito třemi formami

zkráceně tři formy činnosti  motoru ROZJEZD - PROVOZ - VÝKON a dvě formy úhlové rychlosti jako převod mezi nimi

ORIENTACE K NÁKRESŮM:  text pro část tři orientován vzhledem k nákresům zleva doprava a od hora dolů - tedy tzv. evropsky - na rozdíl od většiny jiných popisů s opačnou orientací

3 - 3 ÚHLOVÁ RYCHLOST , MOMENT SÍLY a VÝKON motoru - "zóna 3 VÝKON"

ve výpočtech vyskytuje při výpočtu "výkonu" 
a to přepočtem (přesněji násobením) momentu otáčení

(v tomto případě se patrně více jedná o přepočet, než výpočet)

výkon = úlová rychlost OMEGA  (podruhé ve výpočtech)  x moment otáčení 

výkon = úlová rychlost OMEGA  (podruhé ve výpočtech)  x moment setrvačnosti  x úlová rychlost OMEGA  (poprvé ve výpočtech) 

část 3 - UHLOVÁ RYCHLOST - MOMENT SÍLY A VÝKON

tato část příspěvku spadá do tématického okruhu Mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

3 - 32 ÚHLOVÁ RYCHLOST , MOMENT SÍLY a VÝKON motoru - mezizóna 32  ÚHLOVÁ RYCHLOST PODRUHÉ ve výpočtech

-  výkon přepočtem z momentu síly"

funkce motoru a úhlová rychlost OMEGA

úhlová rychlost OMEGA podruhé pro výpočet výkonu přepočtem z momentu točení, úhlová rychlost OMEGA poprvé pro výpočet momentu síly (momentu točení) přepočtem ze startovacího momentu setrvačnosti

úhlová rychlost "OMEGA" je vlastně frekvence (četnost otáčení, časočetnost) s proměnlivým úhlem 
- jejíž funkce je možno poměrně názorně "demonstrovat" na sešlápnutí pedálu plynu

úhlová rychlost OMEGA se ve výpočtech vyskytuje vlastně dvakrát

část 3 - UHLOVÁ RYCHLOST - MOMENT SÍLY A VÝKON

3 - 2 ÚHLOVÁ RYCHLOST , MOMENT SÍLY a VÝKON motoru- "zóna 2 PROVOZ"

"zona 2" předvýpočet - či souběžný výpočet-

výpočty či přepočty  frekvencí 

"zóna 2" hlavní výpočet

výpočet momentu otáčení násobením úhlovou rychlostí momentu setrvačnosti 

1. výpočet momentu síly motoru

poprvé se "úhlová rychlost omega" 
ve výpočtech vyskytuje při výpočtu "momentu točení" a to přepočtem (přesněji násobením) výchozího - či startovacího "momentu setrvačnosti"

(moment setrvačnosti vlastně odvisí od mechanicko-kinematických vlastností motoru - moment setrvačnosti se počítá na základě znalosti těžiště a rozměrů (tedy poloměru - válce, ozubeného kola)

moment točení = moment setrvačnosti x úlová rychlost OMEGA (poprvé ve výpočtech)

část 3 - UHLOVÁ RYCHLOST - MOMENT SÍLY A VÝKON

3 - 21 ÚHLOVÁ RYCHLOST , MOMENT SÍLY a VÝKON motoru - mezizóna 21  ÚHLOVÁ RYCHLOST POPRVÉ ve výpočtech - MOMENT OTÁČENÍ  přepočtem z MOMENTU SETRVAČNOSTI

"úhlová rychlost omega poprvé ve výpočtech" 
ve výpočtech vyskytuje při výpočtu "momentu točení" a to přepočtem (přesněji násobením) výchozího - či startovacího "momentu setrvačnosti"

úhlová rychlost "OMEGA" je vlastně frekvence (četnost otáčení, časočetnost) s proměnlivým úhlem 
- jejíž funkce je možno poměrně názorně "demonstrovat" na sešlápnutí pedálu plynu

úhlová rychlost OMEGA se ve výpočtech vyskytuje vlastně dvakrát

část 3 - UHLOVÁ RYCHLOST - MOMENT SÍLY A VÝKON

3 - 1 ÚHLOVÁ RYCHLOST , MOMENT SÍLY a VÝKON motoru - "zóna 1"  ROZJEZD

"zona 1" -předvýpočet - či souběžný výpočet-

výpočty či přepočty  frekvencí  - zejména úhlové rychlosti při startu a rozjezdu

"zóna 1" - hlavní výpočet

výpočet momentu setrvačnosti především na základě mechanicko-kinematických  vlastností motoru 

(moment setrvačnosti vlastně odvisí od mechanicko-kinematických vlastností motoru - moment setrvačnosti se počítá na základě znalosti těžiště a rozměrů (tedy poloměru - válce, ozubeného kola)

moment točení = moment setrvačnosti x úlová rychlost OMEGA (poprvé ve výpočtech)

přičemž úlová rychlost OMEGA (podruhé ve výpočtech) nemusí, ale může být totožná s úlovou rychlostí OMEGA (poprvé ve výpočtech)

SHRNUTÍ  ČÁSTI 3  - UHLOVÁ RYCHLOST - MOMENT SÍLY A VÝKON

funkce motoru a úhlová rychlost OMEGA

úhlová rychlost OMEGA podruhé pro výpočet výkonu přepočtem z momentu točení, úhlová rychlost OMEGA poprvé pro výpočet momentu síly (momentu točení) přepočtem ze startovacího momentu setrvačnosti

VÝZNAM ÚHLOVÉ RYCHLOSTI PRO VÝPOČTY  - VÝPOČET VÝKONU Z HLEDISKA ÚHLOVÉ RYCHLOSTI neboli ÚHLOVÉ FREKVENCI K PROMĚNLIVÉMU ÚHLU - což přibližně odpovídá ÚHLU SEŠLÁPNUTÍ PLYNU

MOŽNÉ ZÁMĚNY

úhlová rychlost omega od startu do rozjezdu OMEGA 1 

úhlová rychlost omega od rozjezdu výše OMEGA 2 jenž je současně úhlovou rychlostí  poprvé ve výpočtech tedy výpočtovou veličinoumomentu otáčení Mt k násobení momentu setrvačnosti MI

úhlová rychlost omega podruhé ve výpočtech OMEGÁˇ (s apostrofem) tedy přepočtová veličina pro výkon P  k násobením momentu otáčení MI 
ve výpočtech vyskytuje při výpočtu "výkonu" 
a to přepočtem (přesněji násobením) momentu otáčení

v tomto případě se patrně více jedná o přepočet, než výpočet

přičemž úlová rychlost OMEGA (podruhé ve výpočtech) nemusí, ale může být totožná s úlovou rychlostí OMEGA (poprvé ve výpočtech)

SHRNUTO: ROZJEZD s momentem setrvačnosti  - vlastní PROVOZ  s momentem otáčení a VÝKON  motoru s úhlovou rychlostí jako přepočtovou veličinou mezi těmito třema formami

KONEC ČÁSTI 3  - UHLOVÁ RYCHLOST - MOMENT SÍLY A VÝKON

VLASTNÍ PŘÍSPĚVEK DALŠÍ ĆÁST - ČÁST 4 MATEMATICKÉ FUNKCE

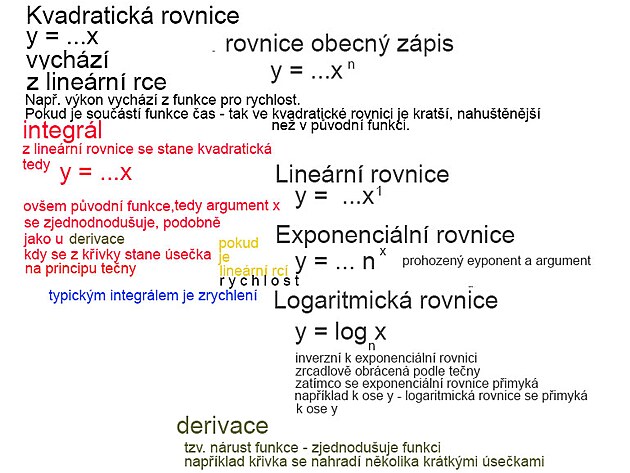
4  MATEMATIKA - INTEGRÁLY A DERIVACE - tři formy činnosti  motoru - ROZJEZD jako derivace nebo podíl - vlastní PROVOZ  jako běžná matematická funkce - rychlost, integrál jako zrychlení a VÝKON  motoru jako kvadratická funkce

funkce, rovnice a integrální a diferenciální počet - exponenciální a logaritmická funkce

rovnice a funkce

malé pojednání o rovnicích, funkcích a veličinách

třeba už z názvosloví při značení funkcí mohou vznikat jisté nejasnosti

rovnice sice není přímo funkce, ale v mnoha případech rovnice a funkce může být totéž

 

část 2XY/ rovnice a funkce - a jejich průběh

rovnice sice není přímo funkce, ale v mnoha případech rovnice a funkce může být totéž

nejprve rovnice -  ovšem s levo - pravým dělením podle stran již jako funkce

Co je to vlastně vyjadřuje rovnice... Na vzdory rovnítka uprostřed neznamená, že levá a pravá strana rovnice vyjadřuje totéž. 

LEVÁ STRANA ROVNICE - souhrnná neznámá "Y" (funkce, zjišťovaný pochod) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu,(zkoumaná veličina, konkrétní výsledek).- výkonná neznámá "x", případně "z" 

LEVÁ STRANA ROVNICE (rychlost) - PRAVÁ STRANA ROVNICE spíš prostředek výpočtu, (zkoumaná veličina - dráha, funkce času). 

druhy rovnic a funkcí 

lineární rovnice s jednou neznámou a to na prvou
kvadratická rovnice - s neznámou - což je zpravidla x na druhou
funkce s x na druhou - teoreticky by se mělo jednat o kvadratickou funkci (toto označení se ale příliš nepoužívá) - pro tuto funkci se zde v příspěvcích používá i nepřesně označení exponenciální funkce 
exponenciální rovnice - s neznámou v exponentu 
logaritmická rovnice - teoreticky by byla příbuzná s exponenciální rovnicí - vlastně by mělo jít o převrácenou exponenciální rovnici
goniometrická rovnice - která zahrnuje funkce sinus a cosinus 

průběh rovnic a funkcí 

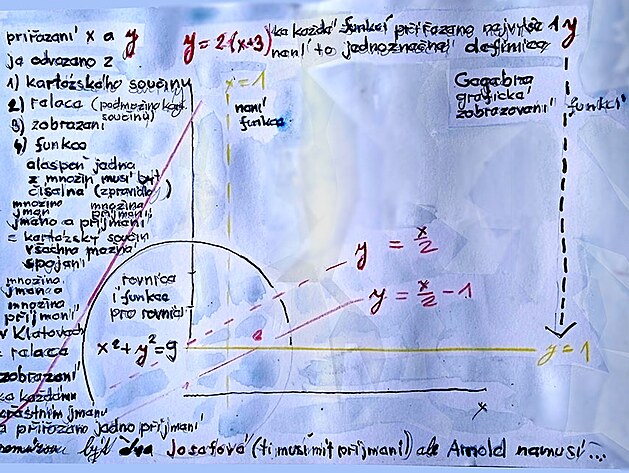
na obrázku níže zobrazeny

žlutě: rovnice x = 1, která by stoupala strmě podél osy y, a pak funkce y = 1, jejíž průběh by byl podél osy x  

červeně: funkce y = x/2 a funkce y = x/2 - 1 obě funkce směřují v úhlu 45st. mezi osami a druhá zmíněná funkce je o jednotku na stupnici posunutá 

dále je zde uvedena kružnice - která je definována vzorcem x na druhou + y na druhou = 9

Funkce a příbuzné matematické záležitosti mohou mít jednak číselný (matematický) zápis - dále jdou zobrazit graficky - a rovněž zpravidla mají nějaký reálný význam - mohou popisovat průběh elektrotechnických veličin - veličin v mechanice - jako například průběh rychlosti  - dále mohou popisovat úplně běžné záležitosti - různé přiřazování souvisejících veličin různých druhů...

KONEC ČÁSTI 4 INTEGRÁLY A DERIVACE A MATEMATICKÉ FUNKCE VE VÝPOČTECH, rozdíl mezi x a y v rovnici a mezi osou X a y v kartézských souřadnicích   

související příspěvky

A11V Rovnice, funkce, derivace, integrály, logaritmy, a Eulerova konstanta - Blog iDNES.cz

Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů AV - Blog iDNES.cz

VLASTNÍ PŘÍSPĚVEKČÁST 5 ČAS A ROZMĚR

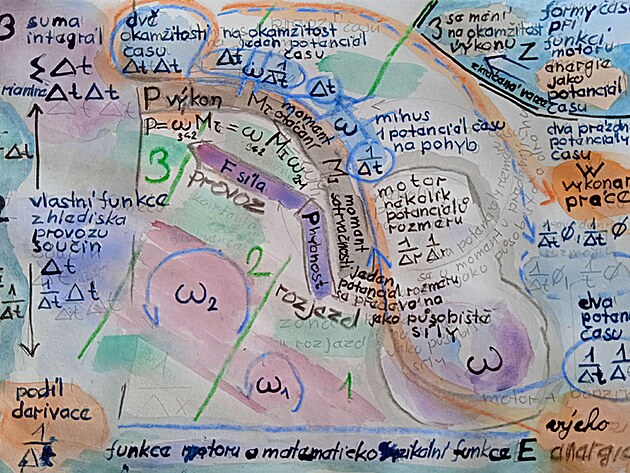
5 VELIČINA ČAS VE VÝPOČTECH - tři formy činnosti  motoru - ROZJEZD - PROVOZ - VÝKON  a  přeměna veličiny času z potenciálu času před jízdou přepočtem přes úhlovou rychlost na okamžitost výkonu

bádání níže bylo již v řadě závěrů překonáno - obsahuje řadu záměn témat - aktuálnější - a snad i přesnější závěry v odkazech 

čas a rozměr ve výpočtech

čas je poměrně obtížně znázornitelná veličina sama o sobě

například ve výkonu se projevuje jako "okamžitost" - přiřazená k provozní ose y - kdežto k časosběrné ose x - jinak také k ose rozměrů se projevuje jako "potenciál času" -- který reflektuje jednak vlastní zařízení - tedy třeba motor a dále i stav pohonných hmot (potenciál času na který je zásoba benzínu)

na ilustraci níže pomyslné předávání potenciálu času  nenastartovaného vozu s palivem na "okamžitost výkonu" (mezi zónou 2 a 3) , případně na moment točení z momentu setrvačnosti mezi "zónou 2 a 1" 

5 - 1  "zóna 1 - START  a ROZJEZD 

5 - 12  "mezizóna 12 - vlastní ROZJEZD - jeden potenciál času se "předává na okamžitost"

úlová rychlost OMEGA  (poprvé ve výpočtech) 

PŘI TĚCHTO VÝPOČTECH SE OBRAZNĚ ZTRÁCÍ JEDEN POTENCIÁL ČASU NA JEDEN OKAMŽIK

úhlová rychlost OMEGA (poprvé ve výpočtech) se před rozjetím označuje 1 - po rozjetí 2

úhlovou rychlost  lze převést na jiné druhy frekvence viz část "2"

5 - 2  "zóna 2 - PROVOZ  - jeden potenciál času se "předává na okamžitost"

souběžný, či předběžný výpočet frekvence

jako určitý přidružený výpočet 

jeden potenciál času se předává na "okamžitost"

úhlovou rychlost  lze převést na jiné druhy frekvence viz část "2"

hlavní výpočet: výpočet síly a momentu  otáčení

jeden potenciál času se předává na okamžitost,

jeden potenciál rozměru se předává na konkrétní působiště síly,

dva potenciály rozměru se předávají na výpočet momentu točení - tedy působiště a dráha

5 - 32  "mezizóna 32" - vlastní  výpočet VÝKONU přepočtem MOMENTU  OTÁČENÍ  - druhý  potenciál času se "předává na okamžitost"

5 - 3  "zóna 3" - VÝKON 

PŘI TĚCHTO PŘEPOČTECH  SE OBRAZNĚ ZTRÁCÍ DRUHÝ POTENCIÁL ČASU NA  OKAMŽITOST VÝKONU

výkon = úlová rychlost OMEGA (podruhé ve výpočtech) x moment otáčení

výkon = úlová rychlost OMEGA (podruhé ve výpočtech) x moment  setrvačnosti x úlová rychlost OMEGA (poprvé ve výpočtech)

úhlovou rychlost OMEGA (podruhé ve výpočtech) při přepočtu momentu otáčení na výkon možno pro odlišení OMEGA (poprvé ve výpočtech) označit na nákresech například apostrovem

shrnutí: podruhé  se "úhlová rychlost omega" 
ve výpočtech vyskytuje při výpočtu "výkonu" 
a to přepočtem (přesněji násobením) momentu otáčení

(v tomto případě se patrně více jedná o přepočet, než výpočet)

KONEC ČÁSTI 5 ĆAS A ROZMĚR VE VÝPOČTECH

k ilustracím 

číslování na nákresech "tři, dva, jedna - start" tedy k výsledku "na levo" z od začátku  v pravo (zóna 3 "cíl", zóna 2 "provoz", zóna 1 "start" - u některých nákresů je však číslování opačné)

 a na závěr znovu obsah a základní náměty příspěvku

rozcestníky

matematika obecně
vnitřní matematika – matematika přepočtů (například úhly)
vnější matematika – matematické funkce (i pro jiné obory)
vnější matematika – matematické funkce (i pro jiné obory) integrální a diferenciální počet 
matematika rychlosti a zrychlení (DAV)
podrozcestník rychlost a zrychlení v letectví 
matematika a kybernetika 
automobilismus, motorismus, cyklistika auto - moto - kolo podle značek se zaměřením na vozy ŠKODA
zemědělské stroje, traktory
mechanika pohybu  
kinematika jako mechanika KFD - linie frekvence - rychlost (linie kinematika - dynamika)
kinematika druhů (aritmetická, aritmeticko - geometrická, deskriptivně - geometrická konematika)
dynamika jako mechanika DPM - dynamika - linie rychlost, moment síly, výkon
mechanika DPMW - porovnání alternativních výpočtů veličin rychlost, výkon, energie, práce
Mechanika DHM - mechanika hybnosti a méně obvyklých veličin (dvojitých momentů) 
mechanika JB - mechanika jeřábů a bagrů - více praktická verze mechaniky hybnosti
statika

obsah vlastního příspěvku

1 POMĚR MEZI OBVODEM KRUŽNICE jako východisko pro další přepočty -  Ludolfovo číslo a  rozměr úhlu jeden RADIÁN

2 mechanika KFD - kinematika-  frekvence a dynamika - úhlová rychlost a rychlost

ÚHLOVÁ RYCHLOST, OTÁČKY ZA MINUTU  a další  druhy veličiny FREKVENCE ve výpočtech funkce motoru a převody mezi nimi

3 mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

ÚHLOVÁ RYCHLOST a TŘI FORMY ČINNOSTI motoru - ROZJEZD s momentem setrvačnosti  - vlastní PROVOZ  s momentem otáčení a VÝKON  motoru sÍ ÚHLOVOU RYCHLOSTÍ  jako přepočtovou veličinou mezi těmito třemi formami

4 MATEMATIKA - INTEGRÁLY A DERIVACE - tři formy činnosti  motoru - ROZJEZD jako derivace nebo podíl - vlastní PROVOZ  jako běžná matematická funkce - rychlost, integrál jako zrychlení a VÝKON  motoru jako kvadratická funkce

5? Mechanika DPM - dynamika - přepočty sil a momentů (rozjezd - jízda  výkon)

ČAS A ROZMĚR VE VÝPOĆTECH a TŘI FORMY ČINNOSTI motoru   - ROZJEZD - PROVOZ - VÝKON  a  přeměna veličiny času z potenciálu času před jízdou přepočtem přes úhlovou rychlost na okamžitost výkonu - veličina čas se ve výpočtech vyskytuje ve jmenovateli - kokrétněve frekvenci - časem tedy dělí - na ose x jakoby čas měl hodnotu jedna - a následně jakoby se interval zkracoval - v případě výkonu - promítaného obvykle na osu y se veličinou čas dělí dokonce dvakrát - jelikož jde o exponenciál, či integrál