C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů
obsah
část 1
Oblouková míra - stupně, Ludolfovo číslo a radiány (původní příspěvek)
rozcestník "radián" a matematika doplňkových výpočtů
část 2
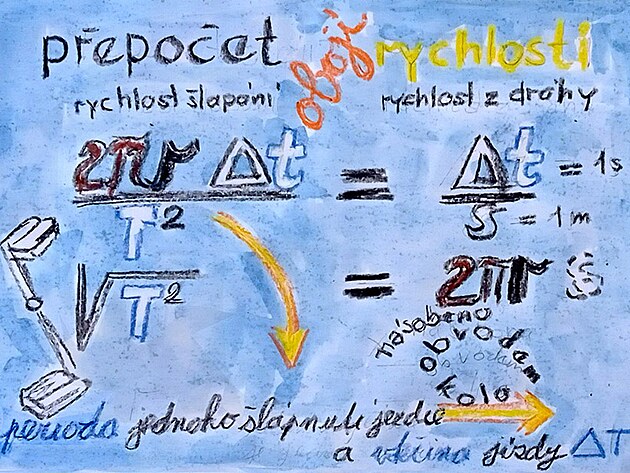
matematika ve strojírenství - přepočty vstupní a výstupní rychlosti bicyklu
část 3
alternativní výpočet rychlosti z dráhy nebo frekvence
část 4
cyklistika a motorizmus podle značek (Cyklistka 1)
+ motocykly "Z" a rozcestník Zbrojovka Brno
NEJPRVE ROZCETNÍKY
ROOZCESTNÍK MATEMATIKA PŘEPOČTY ÚHLŮ (vnitřní matematika – matematika přepočtů)
Mechanika A/ KDF rychlá nákladní vozidla a jejich rozjezd 1 - přečepočet různých druhů frekvence při rozjedu - úhlová k radiánu, celoúhlová frekvence k 360 a RPM - otáčky za minutu " - Blog iDNES.cz který tvoří dvoupříspěvek s příspěvkem Mechanika A/ KFD - Ludolfovo číslo a radián - přepočty různých druhů frekvence - Blog iDNES.cz
ROZCESTNÍK MATEMATIKA FUNKCÍ a INTEGRÁLŮ (vnější matematika – matematické funkce -i pro jiné obory)
ROZCESTNÍK MATEMATICKÁ MECHANIKA
ROZCESTNÍK Mechanika KDF (kinematika - dynamika - frekvence) - výpočet rychlosti cestou frekvence
rychlé vozy "velká kola" - kola s velkou obvodovou rychlostí která se zvětšuje právě směrem k obvodu Mechanika KFD / DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola - Blog iDNES.cz
"podrozcestník pro rozjezd" - zejména nákladních vozů
Mechanika DPM/W výkon okamžitý z frekvence, nebo statistický z práce - nákladní vozy - Blog iDNES.cz
odkaz na ROZCESTNÍK "auto - moto - kolo" Mechanika A/ KFD - Ludolfovo číslo a radián - přepočty frekvence, rozjezd vozů 2 - Blog iDNES.cz
podrozcestník KDF bicyklu - kinematika a dynamika zaměřená na výzkum rychlosti bicyklu
"cyklistika 1 (motokola 1)" bicykly, mopedy a motocykly podle továrních značek Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů (tento příspěvek) součástí příspěvku je také alternativní výpočet rychlosti z frekvence nebo dráhy, a také výpočet vstupní a výstupní rychlosti bicyklu
"cyklistika 2" cyklistika a motorismus pohonů a závodů Mechanika KFD 2 - pomaluběžný nebo rychloběžný motor, cyklistické závody - Blog iDNES.cz
ROZCESTNÍK RYCHLOST a ZRYCHLENÍ DAV (PM)
Letecké měřící přístroje a odpovídající veličiny, letiště Žatec a Mig 29 - Blog iDNES.cz.cz především teoretická analýza měření rychlosti (z výkonu nebo dráhy?)
Mechanika KFD 2 - pomaluběžný nebo rychloběžný motor, cyklistické závody - Blog iDNES.cz porovnání dvou metodik výpočtu rychlosti - převodem z frekvence a rychlost jako dráha lomeno čas
Mechanika A/ DAV (PM) - matematika slovesně, zrychlení neboli vzlet 1, katalog letišť - Blog iDNES.cz zde například rozdíl mezi výukou matematiky na základních, středních a vysokých školách
ROZCESTNÍK Mechanika DPM (dynamika výkonů a momentů)
přepočet sil, momentů, rychlostí na ose i na obvodu a výkonu (mechanika DPM) na kole vozu i celém vozidle
"první díl" Mechanika DPM1 - Výkon, nebo točivý moment - proč má traktor velké zadní kolo a je pomalý? - Blog iDNES.cz (přepočet síla a momenty) - v části 3 odkazovaneho příspěvku
"druhý díl" pokračování přepočtů "druhý díl" - se zaměřením úhlová rychlost, moment setrvačnosti a moment otáčení na ose - a síla na obvodu kola v příspěvku Mechanika DPM 3 /W moment setrvačnosti /úhlová rychlost - moment síly - síla / výkon okamžitý z frekvence a statistický z práce - nákladní vozy 3 - Blog iDNES.cz(v části 3 odkazovaného příspěvku)
a další pokračování "třetí díl" - kde přepočty doplní i přepočet úhlová rychlost - rotační rychlost a síla na obvodu Mechanika KFD / DAV - frekvence, rychlost, zrychlení / kinematika fotbalového míče / proč rychlé vozy mají velká kola - Blog iDNES.cz
inverzní moment síly, který se zvětšuje k obvodu (?) neblaze proslulá hranatá okénka u letounu Comet de Havilland kde se na okrajích vytvářely mikroskopické praskliny Paní Simpsonová a Goethe / De Havilland DH 106 Comet - Blog iDNES.cz
ROZCESTNÍK ALTERNATIVNÍCH VÝPOČTŮ VELIČIN VÝKON PRÁCE,ENERGIE, RYCHLOST Mechanika DPMW
například rychlosti buď z dráhy nebo z frekvence
Letecké měřící přístroje a odpovídající veličiny, letiště Žatec a Mig 29 - Blog iDNES.cz.cz především teoretická analýza měření rychlosti (z výkonu nebo dráhy?)
Mechanika KFD 2 - pomaluběžný nebo rychloběžný motor, cyklistické závody - Blog iDNES.cz porovnání dvou metodik výpočtu rychlosti - převodem z frekvence a rychlost jako dráha lomeno čas
a také hlavní rozcestník pro mechaniku pohybu Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů - Blog iDNES.cz
alternativní výpočty veličin v mechanice -okamžitá a statistická rychlost, čímž se zabývá především příspěvek Oblouková míra - stupně, Ludolfovo číslo a radiány a přepočet rychlosti vstup - výstup - Blog iDNES.cz tedy alternativní výpočet rychlosti,tento příspěvek
veličinou rychlost by se ovšem měl také zabývat příspěvek
Nádraží a vlak - rychlost a zrychlení - mechanika integrálních a diferenciálních počtů - Blog iDNES.czzde ovšem pojednáno nejen o vlastní rychlosti ale i jejím rozdělením na část rovnoměrnou a rovnoměrně zrychlenou - zda se jedná o pohyb rovnoměrný, či zrychlený...
veličinu výkon by zase měl pojednávat příspěvek Mechanika DPM/W výkon okamžitý z frekvence, nebo statistický z práce - nákladní vozy - Blog iDNES.cz
VLATNÍ PŘÍSPĚVEK
část 1
Oblouková míra - stupně, Ludolfovo číslo a radiány - rozcestník matematika doplňkových výpočtů
EULEROVA KONSTANTA, sinus, cosinus A11V Rovnice, funkce, derivace, logaritmy a Eulerova konstanta - Blog iDNES.cz
RADIÁN 1A
výchozí rozcestník pro mechaniku pohybu automobilů a rozcestník pro matematiku úhlů, měr a přepočtů Mechanika A/ KFD : kinematika (frekvence), dynamika (úhlová a obvodová rychlost) - Škoda - Blog iDNES.cz původním názvem Mechanika A/ KFD - Ludolfovo číslo a radián - přepočty různých druhů frekvence - Blog iDNES.cz
RADIÁN 1C Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů (tento příspěvek)
RADIÁN 3 Mechanika A3/KFD - radián, frekvence, rozjezd a výkon sanitky, rozcestník Avia - Blog iDNES.cz?
malá anotace
DÉLKA OBLOUKU = DÉLKA OBLOUKU KRUHOVÉ VÝSEČE O ÚHLU JEDEN RADIÁN krát ÚHEL KONKRÉTNÍHO ZJIŠŤOVANÉHO OBLOUKU
DÉLKA OBLOUKU = DÉLKA OBLOUKU KRUHOVÉ VÝSEČE O ÚHLU JEDEN RADIÁN (délka tohoto obloUku je tatáž jako poloměr) krát ÚHEL KONKRÉTNÍHO ZJIŠŤOVANÉHO OBLOUKU
Informace především na základě diskusí
Obecný vztah pro výpočet délky kruhového oblouku
L=k*R*?
(konstanta krát poloměr krát úhel).
L(délka kruhového oblouku)=k(konstanta pro přepočet dle konkrétní úhlové jednotky) krát r(poloměr) krát ? (úhel - dle té či které úhlové jednotky)
Ta konstanta se mění podle toho, v jakých úhlových jednotkách dosazujeme velikost úhlu. Pokud dosazujeme ve stupních, má konstanta velikost
k=?/180
pokud dosazujeme v radiánech, má konstanta význačnou hodnotu k=1
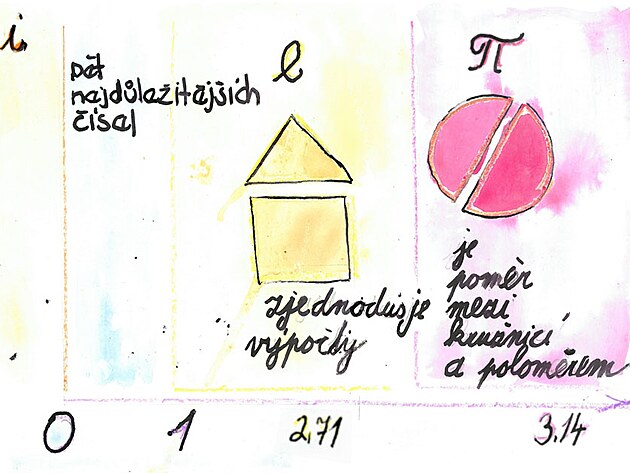
PROČ SE POUŽÍVAJÍ RADIÁNY...
Co vlastně znamená 2? ve výpočtu obvodů. Číslo ? se používá proto, že pro řadu "obvyklých" úhlů má přesná hodnota v radiánech nekonečný desetinný rozvoj. Pro přesné symbolické vyjádření je proto dobré použít krátký zástupný symbol ? nebo jeho násobek. Je to ale jen informace, jak má to číslo vypadat , aby si každý mohl zvolit, jak přesně chce počítat. Pro obecné úhly se použije konkrétní číselná hodnota.
Pokud chcete délku oblouku, vyjádřeného v různých rovinných úhlových měrách se známým poloměrem je výpočet
délka oblouku L [v metrech] = úhel [ve stupnich] * poloměr kružnice R [v metrech] * 0,0174533
L [v metrech] = úhel [v dekadech] * R [v metrech] * 0,015708
L [v metrech] = úhel [v hodinach] * R [v metrech] * 0,5236
L [v metrech] = úhel [v ? a radiánech] * R [v metrech] * 1
L [v metrech] = úhel bez jednotek v ? * R [v metrech] * 1 de facto stejná formule jako výše jen nepíší radiány
Z výše uvedených výpočtů je jasné, proč se používají radiány: výpočet dá nejméně práce. Násobení jedničkou je nejsnazší. U ostatních výpočtů je třeba násobit konstantami s nekonečnými desetinnými rozvoji, které jsou pro jednoduchost zaokrouhlena..
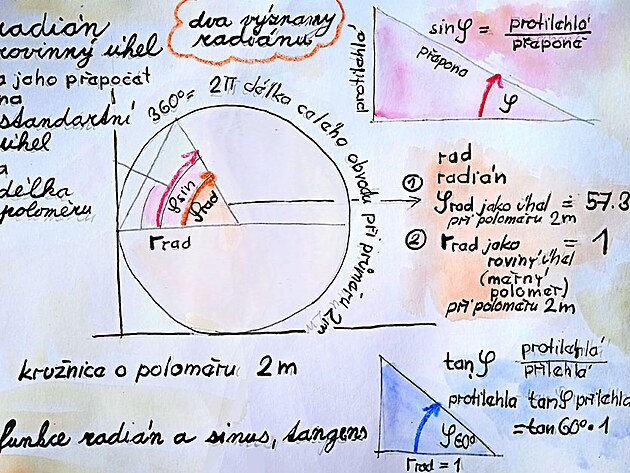
RADIÁN - ROVINNÝ ÚHEL A JEHO SROVNÁNÍ S ROVNOSTRANNÝM TROJÚHELNÍKEM
Stupeň (úhlový) je jednotkou velikosti ROVINNÉHO ÚHLU.
Radián je také jednotkou velikosti rovinného úhlu - ovšem možno konstatovat - že označení rovinný se v případě radiánu zdůrazňuje poněkud více - než v případě jiných úhlových jednotek jako stupně, nebo gradiány.
Na základě uvedenýh zjištění by se dalo SHRNOUT - že délka oblouku se počítá násobení poloměru a velikosti úhlu dle různých přepočtů podle konkrétní míry.
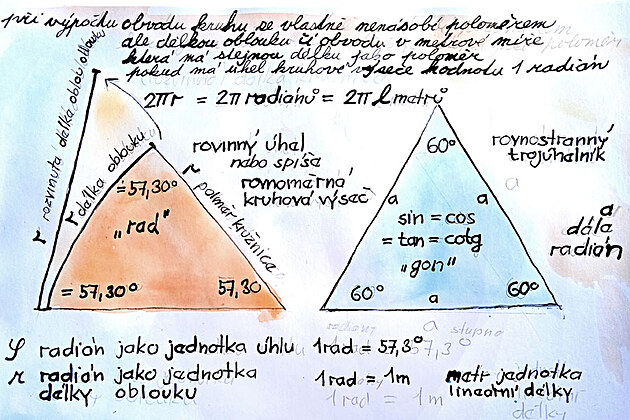
A co třeba srovnat kruhovou výseč danou právě úhlem radiánu (tedy 57.3 přeočteno na stupně) a rovnostranný trojúhelník o rozměrech 60 stupňů.
V tomto případě vyjdou geometrické útvary do určité míry se podobající.
Zajímavosti rovnostranného trojúhelníku je i fakt - že gonimetrické funkce sínus, kosínus, tangens, kotangens v tomto případě nabývají takřka stejnou hodnotu, dá se konstatovat, že vzniká jakási univerzální goniometrická funkce - kterou by bylo možno označit například zkratkou "Gon".(stejnou velikost mají jen strany trojúhelníku a úhly - hodnoty funkcí se liší upraveno na základě poznámek).
Odstavec výše - rovnostranný trojúhelník je neplatný - jelikož funkce sín, cos atd platí pouze pro pravoúhlý trojúhelník.(oprava na základě poznámek)
Kruhová výseč o úhlu "radián" je útvar velmi připomínající rovnostraný trojúhelník a dokonce délka oblouku (oblouk nahrazuje vnější stranu trojúhelníku) tedy délka oblouku rozvinutého do délky je úplně stejná jako délky zbývajících stran - tedy vlastně POLOMĚRU kružnice, či kruhové výseče.
Z čehož plyne: při výpočtu délky kružnice - nebo déky obloku (kruhové výseče)
se nenásobí poloměr - ale délka obloku (který je zde vymezen úhlem o rozměru jeden radián)
DÉLKA OBLOUKU = DÉLKA OBLOUKU KRUHOVÉ VÝSEČE O ÚHLU JEDEN RADIÁN krát ÚHEL KONKRÉTNÍHO ZJIŠŤOVANÉHO OBLOUKU
DÉLKA OBLOUKU = DÉLKA OBLOUKU KRUHOVÉ VÝSEČE O ÚHLU JEDEN RADIÁN (délka tohoto oblouku je tatáž jako poloměr) krát ÚHEL KONKRÉTNÍHO ZJIŠŤOVANÉHO OBLOUKU
z uvedených fakt tedy vyplývá
RADIÁN je
1. jednotka úhlu 1 rad ´= 57.30 st
2. jednotka délky oblouku 1 rad ´= 1 metr přepočet obloukové délky z lineární délky
(3. radián je pravděpodobně i funkce pro výpočet délky oblouku - obdoba goniometrických funkcí)
PROČ TEDY RŮZNICE V INERPRETACI RADIÁNU?
Možná někdo jiný v úvozovkách "vymyslel" radián jako úhlovou jednotku a někdo jiný zase definici.
navazující příspěvek Mechanika A/ KFD - Ludolfovo číslo a radián - přepočty různých druhů frekvence - Blog iDNES.cz
část 2
matematika ve strojírenství - přepočty vstupní a výstupní rychlosti bicyklu
matematika ve strojírenství
Kdo se například o svém volnu trochu zajímá obory mechaniky - si může povšimnout, že poměrně mnoho veličin se zde vyskytuje ve dvojicích. Například výkon se počítá jako násobek rychlost krát síla - což - pokud se jedná a jeden systém - například automobil veličiny nijak zásadně rozdílné - a pokud třeba nějaký zanícený matematik chce obě veličiny vzájemně porovnat - může se stát, že po mnoha hodinových výpočtech dojde k téměř té samé veličině - odlišující se jenom nějakým přepočtovým koeficientem.
jak již bylo zmíněno - na rozdíl od statiky nebo dynamiky - "kinematika" nepřináší výsledky v cifrách - ale spíše jenom analyzuje
/ jinak konkrétnější variantou kinematiky - například určení stupňů volnosti stavebních strojů - nebo uzavřených mechanismů - například čerpadel, se zde zabývá jiný příspěvek - například Dálniční most
část 3
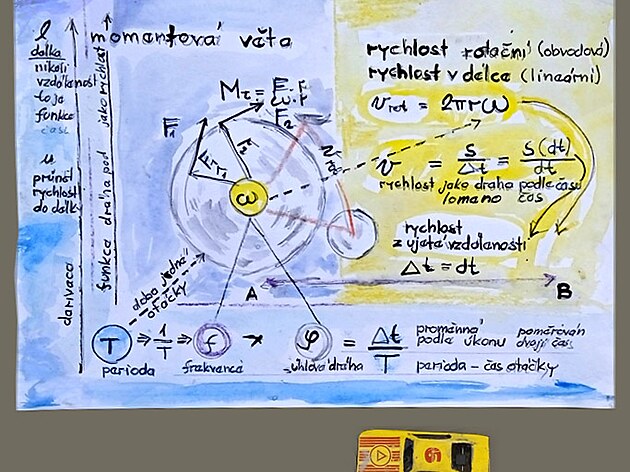
alternativní výpočty rychlosti - z dráhy a frekvence
/momenty - tedy moment setrvačnosti, otáčení a výkon ovšem mají "sídlo" na ose kola/
rychlost lze tedy standartně spočítat jako dráha lomeno čas - stejný výsledek by ovšem měl být dosažen, počítala by se rychlost přepočtem z frekvence pohonu vozidla
-rychlost jako veličina v dynamice - síla krát páka
- (statistická)rychlost- dráha lomeno čas
v obou případech má výsledná rychlost stejné jednotky - třeba metry za sekundu - nebo kilometry za hodinu
v případě nějakého vozidla lze předpokládat, že se měří okamžitá rotační rychlost (nikoli rychlost z ujeté vzdálenosti) - a tato rotační rychlost se navíc vyjadřuje jako lineární
statistická rychlost - dráha lomeno čas - je sice určitým zjednodušením této veličiny - ale zase nepřináší příliš informací o podstatě této veličiny
lze předpokládat
že hodnota - co se měří pro tachometr
je na tachometru zobrazeno se dvěma přepočty
- jednak z rychlosti na základě dynamiky na základě síla x páka na statistickourychlost v kilometrech za hodinu - jejíž průměrná hodnota by odpovídala podílu ujeté dráhy a doby jízdy
- jednak z rotační rychlosti pohonu (nebo jiného otáčejícího se elementu) na lineární rychlost celého vozu
veličinou rychlost by se ovšem měl také zabývat příspěvek
zde ovšem pojednáno nejen o vlastní rychlosti - jak ji vnímá třeba cestující ve vlaku - ale také vjemy cestujícího na nástupišti - neboť tak to nepřímo nazíraná veličina vlastně není rychlostí - ale veličinou která vychází spíše z dráhy, nebo ještě přesněji - spíše s délky vlaku
dále je zde pojednáno zde ovšem pojednáno nejen o vlastní rychlosti ale i jejím rozdělením na část rovnoměrnou a rovnoměrně zrychlenou - zda se jedná o pohyb rovnoměrný, či zrychlený...
část 4
cyklistika a motorismus podle značek
cyklistika, motorismus a automobilismus podle značek
| Původní Masarykův okruh a Velká cena 1984 - Blog iDNES.cz | Jawa | |
| https://www.facebook.com/media/set/?set=oa.2299368560279596&type=3 | ||
| Velká cena Brna a motocykly Kawasaki - Blog iDNES.cz | Kawasaki |
Tripol Rokycany a žst. Kralice nad Oslavou
Tripol Rokycany
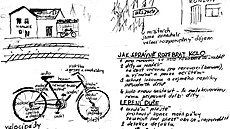
Jak správně rozebrat kolo pro restaurování
pro renovaci se kolo rozebere do šroubků
díly se rozdělí (třeba i barevně) - na díly určené k výměně, renovaci a pouze očištění
lepení duše
1. sundání pláště - sundání pláště - prohnitý konec montážní páky zasunout pod plášť tak aby se nepoškodil
2. detekce defektu (např. vložením pláště do vody)
3. lepení
4. kontrola pláště
motokola Zbrojovka - značky "Z" - neboli "Zetky"
rozcestník Zbrojovka a Zetor
Cesty elektrické energie 11 - rozvody a jištění v průmyslu (Zetor a Zbrojovka) - Blog iDNES.cz - rozcestník Zbrojovka, Zetor, Brno a elektrotechnika
V zajetí počítačů 6 "h" - jak zprovoznit počítač technicky, telekomunikační úřad Brno - Blog iDNES.cz počítače nejen ze Zbrojovky
Jak se připojit k internetu 10 - Ovládání počítače, programy , přenos , internetové účty - Blog iDNES.cz počítače nejen ze Zbrojovky
motocykly podle značek C1 Mechanika A/DPMW: stupně, Ludolfovo číslo radiány - přepočet rychlosti, značky bicyklů (tento příspěvek)
železniční a tramvajová trať Brno Černovice přestup - Líšeň Co mi prozradily tramvajové zastávky v Brně - aneb malé kovové stavby - Blog iDNES.cz
továrna ESKA a jízdní kola a motokola ESKA
Pražská 2756/20, 35002 Cheb, Česko - nyní VEKTRA - okna a dveře
Eska byla pravděpodobně nejznámějším výrobcem kol v Čechách, už také proto, že název přetrval více režimů a víc než tři čtvrtě století. Jeho zakladatelé, opavský Slezan Ambros Swetlik a Němec Heinrich Kastrup, byli zaměstnáni v chebském Premieru a v roce 1911 se rozhodli osamostatnit.
Do nového závodu, který nejprve nazvali ELITE, přetáhli několik zaměstnanců od Premiera a začali s výrobou jízdních kol. Už v roce 1914 jich stačili vyrobit 21 000 a v témže roce také několik kol s pomocným motorkem. Zhruba v té době firmu přejmenovali na ES-KA, podle foneticky vyslovených počátečních písmen svých jmen: Es – Swetlik, Ká – Kastrup.
Asi od roku 1928 nabízeli některé zesílené typy kol s přídavným motorkem Sachs 75. V roce 1935 začali vyrábět malé motocykly Eska Mofa (Motorfahrrad) s motorem Sachs 98. Celý motocykl vážil 50 kg a jel 60 km/h. Podvozek byl samostatně konstruován, nešlo tedy o přizpůsobený velocipéd. Ten byl velmi oblíbený, zejména také proto, že k jeho provozování nebylo třeba řidičské oprávnění, byl osvobozen od daně a mohl být řízen od 15 let. V roce 1939 však jeho výroba skončila a po válce byla obnovena už jen výroba kol.
Swetlik a Kastrup, dva nerozluční přátelé, zemřeli v roce 1932 a 1930. Po celý život byli aktivní, v roce 1922 založili v Rokycanech další továrnu na kola Tripol (viz první článek), která rovněž v určitém období vyráběla motorová kola.
Za zmínku ještě stojí, že Eska byla po roce 1948 závodem České Zbrojovky Strakonice, ale od roku 1950 byla samostatná a pohltila i závod Premier. V sedmdesátých letech uvažovala znovu o motorizaci svých kol. V úvahu přicházely italské motory, ale z projektu sešlo.
Eska - montáž motocyklů o vyšším objemu
Premier o obsahu 500 ccm (SV), který byl vyroben v roce 1932 ve firmě ESKA Cheb. Je zřejmé, že se firma zabývala i výrobou resp. montáží motocyklů u vyšším objemu motoru, nejen motokoly. Pokud si pamatuji, na karteru motoru byl odlit znak Škoda, ráfky nesly označení Dunlop, karburátor byl od firmy Binks, převodovka nesla název Archer. Třístupňové ruční řazení na bandasce
a cyklistický výrobce ze Švédska "WMX"
jízdní kola WMX ze Švédska (WMX cyklare) ovšem mělo by se jednat spíš o výrobce motocyklů WMX STORE | Zakládáme si na osobním přístupu a kvalitním servisu (wmx-store.cz)
přívěsný vozík WMX
zcela zapomenutý výrobce jízdních kol z časů první republiky
FNB Frank und Neufield Brünn
a měšťanský pivovar Bíteš
JAWA
mopedy Stadión
elektrokola Jízdní kola | vidaXL.cz
Jan Tomášek
Dálniční most přes Křešické údolí 3 - kinematika stavebních strojů a stavba mostů

Příspěvek by se měl zabývat především oborem zvaný kinematika - což je poměrně důležitý předmět ve stavebnictví a strojírenství - i když na rozdíl od statiky nebo dynamiky - nepřináší výsledky v cifrách - ale spíše jenom analyzuje
Jan Tomášek
Kamna na piliny - "piliňák"

Kamna na piliny mohou být součástí stolařských dílen, nebo provozoven kde se hodně brousí, hobluje - vznikají piliny a hobliny a mohou sloužit třeba k běžnému topení.
Jan Tomášek
Sněhový pluh KSP 411 / LPO 411 S - užitková železniční vozidla, uhlí a důlní lokomotivy
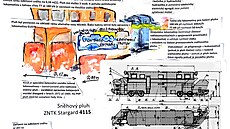
Když zasněží, a trať se stane skrze závěje nesjízdnou neznamená, že by vlaky vůbec neměly vyjet. Ve větších železničních stanicích jsou zpravidla pro tento účel k dispozici různá speciální železniční vozidla - třeba sněhové pluhy.
Jan Tomášek
Cesty energie 2E - jak platit za elektřinu QR kódem, elektřina, plyn a ekonomika, HE Most

Příspěvek by měl pojednávat především o administrativě a ekonomice - především z hlediska spotřebitele - jak se za elektřinu vlastně platí. Ekonomika by měla být pojednána rovněž z hlediska výroby a distribuce.
Jan Tomášek
Mechanika KFD 1 DAV - frekvence, rychlost, zrychlení / proč rychlé vozy mají velká kola
Dva obory mechaniky pohybu - kinematika a dynamika - dá se říci odlišuje právě frekvence a rychlost - tedy od zvuků periody, přes frekvenci a pootočení - dále přes rychlost úhlovou, rotační až po lineární rychlost, atlas Škoda.
| Další články autora |
Tři roky vězení. Soud Ferimu potvrdil trest za znásilnění, odvolání zamítl
Městský soud v Praze potvrdil tříletý trest bývalému poslanci Dominiku Ferimu. Za znásilnění a...
Moderní lichváři připravují o bydlení dlužníky i jejich příbuzné. Trik je snadný
Premium Potřebujete rychle peníze, pár set tisíc korun a ta nabídka zní lákavě: do 24 hodin máte peníze na...
Takhle se mě dotýkal jen gynekolog. Fanynky PSG si stěžují na obtěžování
Mnoho žen si po úterním fotbalovém utkání mezi PSG a Barcelonou postěžovalo na obtěžování ze strany...
Školu neznaly, myly se v potoce. Živořící děti v Hluboké vysvobodili až strážníci
Otřesný případ odhalili strážníci z Hluboké nad Vltavou na Českobudějovicku. Při jedné z kontrol...
Prezident Petr Pavel se zranil v obličeji při střelbě ve zbrojovce
Prezident Petr Pavel se při střelbě na střelnici v uherskobrodské České zbrojovce, kam zavítal...
Odvrátili jsme dronový útok na Minsk z území Litvy, tvrdí Bělorusko
Šéf běloruské tajné služby (KGB) Ivan Tertel ve čtvrtek uvedl, že se podařilo zmařit dronový útok...
Ministerstvo vyčlenilo vakcíny pro těhotné. Válek apeluje na přeočkování dětí
V Česku stále rapidně přibývá případů černého kašle. „Registrujeme 956 nových případů,“ řekla...
„Není podstatné být vidět, ale mít výsledky.“ Politici reagují na konec ministryně
O demisi ministryně pro vědu, výzkum a inovace Heleny Langšádlové (TOP 09) byl premiér Petr Fiala...
Studentky rozrušila přednáška psycholožky, tři dívky skončily v nemocnici
Na kutnohorské střední škole zasahovali záchranáři kvůli skupině rozrušených studentek. Dívky...
- Počet článků 192
- Celková karma 0
- Průměrná čtenost 1043x